2024/2/17に開催されたABC340のD問題 Only one of twoの自分用解説です。
自分は解けませんでした…

問題

正整数N,M,Ｋ が与えられます。ここで、Ｎと Ｍ は異なります。
正の整数であって、ＮとＭのうち ちょうど一方のみ で割り切れる数のうち小さい方からＫ番目のものを出力してください。

考えたこと

・多分　二分探索で解くんだろう
・「ＮとＭの一方のみで割り切れる数」をどうやって用意するんだろう？

結局「ＮとＭの一方のみで割り切れる数」をどう作るか考えつかずに時間切れ。

サンプルコード(解説ページからコピペ)

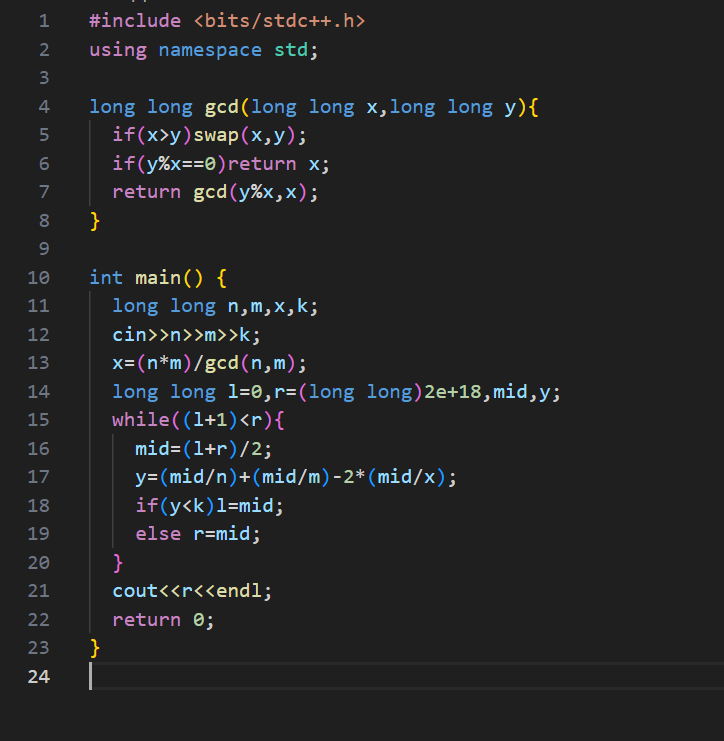
大事そうなところ解説

二分探索は合ってましたが、大事なところを勘違いしてました…
自分は「ＮとＭの一方のみで割り切れる数」の配列を作ろうと悩んでいたのですが、求めたいのは条件を満たす「個数」なので、そんな配列要らないんですね。(そんな配列があったら二分探索しなくていいし)

条件を満たす「個数」は、「Nの倍数 + Mの倍数 – NとMの最小公倍数 * 2」なので、17行目のような式になります。

line 4~8 : 渡された２つの整数の最大公約数を求めています。
　　　　 最小公倍数 = N * M / NとMの最大公約数　だから、最大公約数が必要なんですね。

反省

問題文読み違えというか、解釈の勘違いというか…
もったいないですね。

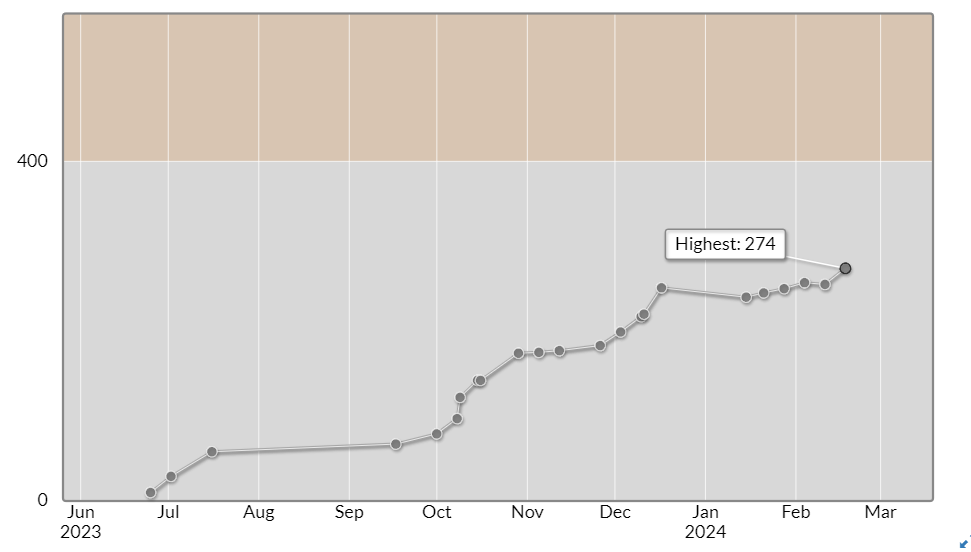
Cまで解けたのでHighest更新！
Cを安定して解けるかが茶色への課題です。